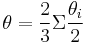Ligand cone angle
The ligand cone angle (also known as the Tolman cone angle or θ) is a measure of the size of a ligand. It is defined as the solid angle formed with the metal at the vertex and the hydrogen atoms at the perimeter of the cone (see figure). Tertiary phosphine ligands are commonly classified using this parameter, but the method can be applied to any ligand. The term cone angle was introduced by Chadwick A. Tolman, a research chemist at Dupont. Originally applied to phosphines, these cone angles were originally determined by building scale models of these phosphines, and physically measuring the angle of the cone by a home-made device.[1][2][3]
Contents |
Asymmetric cases
The concept of cone angle is most easily visualized with symmetrical ligands, e.g. PR3. But the approach has been refined to include less symmetrical ligands of the type PRR'R" as well as diphosphines. In such asymmetric cases the substituent angles half angles, θi/2, are averaged and then doubled to find the total cone angle, θ. In the case of diphosphines the θi/2 of the backbone is approximated as half the chelate bite angle assuming a bite angle of 74, 85, 90 deg. for diphosphines with methylene, ethylene, and propylene back bones respectively.
Variations
The Tolman cone angles assume empirical bond data and defines the perimeter as the maximum possible circumscription of an idealized free spinning substituent. In contrast the solid-angle concept derives both bond length and the perimeter form empirical solid state crystal structures.[4][5] There are advantages to each system.
Application
The concept of cone angle is of practical importance in homogeneous catalysis because the size of the ligand affects the reactivity of the attached metal center. In a famous example, the selectivity of hydroformylation catalysts is strongly influenced by the size of the coligands.
Cone angle values
Cone angles of common phosphine ligands in degrees:
| Ligand | Angle (°) |
|---|---|
| PH3 | 87 |
| PF3 | 104 |
| P(OCH3)3 | 107 |
| dmpe | 107 |
| depe | 115 |
| P(CH3)3 | 118 |
| dppm | 121 |
| dppe | 125 |
| dppp | 127 |
| P(CH2CH3)3 | 132 |
| dcpe | 142 |
| P(C6H5)3 | 145 |
| P(cyclo-C6H11)3 | 170 |
| P(t-Bu)3 | 182 |
| P(C6F5)3 | 184 |
| P(2,4,6-Me3C6H2)3 | 212 |
One remarkable feature becomes clear from these data: some ligands occupy more than half of the coordination sphere of a metal center.
See also
- Bite angle
- Steric effects (vs. electronic effects)
- Tolman electronic parameter
References
- ^ Tolman, Chadwick A. (1970-05-01). "Phosphorus ligand exchange equilibriums on zerovalent nickel. Dominant role for steric effects". J. Am. Chem. Soc. 92 (10): 2956–2965. doi:10.1021/ja00713a007.
- ^ Tolman, C. A.; W. C. Seidel, L. W. Gosser (1974-01-01). "Formation of three-coordinate nickel(0) complexes by phosphorus ligand dissociation from NiL4". J. Am. Chem. Soc. 96 (1): 53–60. doi:10.1021/ja00808a009.
- ^ Tolman, C. A. (1977). "Steric Effects of Phosphorus Ligands in Organometallic Chemistry and Homogeneous Catalysis". Chem. Rev. 77 (3): 313–48. doi:10.1021/cr60307a002.
- ^ Immirzi, A.; A. Musco (1977). "A method to measure the size of phosphorus ligands in coordination complexes". Inorganica Chimica Acta 25: L41–L42. doi:10.1016/S0020-1693(00)95635-4. http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6TG5-43B8S8H-KF&_user=10&_coverDate=12%2F31%2F1977&_rdoc=60&_fmt=high&_orig=browse&_srch=doc-info(%23toc%235245%231977%23999749999%23253901%23FLP%23display%23Volume)&_cdi=5245&_sort=d&_docanchor=&_ct=107&_acct=C000050221&_version=1&_urlVersion=0&_userid=10&md5=59cd327789cffac36f7a8627f88eaec5. Retrieved 2009-12-04.
- ^ Niksch, Tobias; Helmar Görls, Wolfgang Weigand (2009). "The Extension of the Solid-Angle Concept to Bidentate Ligands". European Journal of Inorganic Chemistry 9999 (9999): NA. doi:10.1002/ejic.200900825.